| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- react hook
- 장고
- 프로그래머스 완전탐색
- design pattern
- react firebase
- NextJS
- websocket
- JavaScript
- 프로그래머스
- 프로그래밍 언어론
- 데이터모델링과마이닝
- 디자인 패턴
- codesandbox
- 자바 공부
- 자바
- Java
- react
- 리액트 훅
- 백준
- 컴퓨터 네트워크
- 코틀린
- vanillaJS
- 코딩테스트 고득점 Kit 완전탐색
- useState
- useEffect
- 리액트
- 코딩테스트 고득점 Kit
- 자바스크립트
- 프로그래머스 자바
- React JS
- Today
- Total
기록하는 개발자
[데이터모델링과마이닝] 7. 정규화(Normalization) 본문
[ 이상(anomaly) ]
· DML 연산 시 이상(anomaly)이 발생할 수 있다.
· anomaly는 데이터의 종속성과 중복성에 의해 발생 한다.
· 해결 : attribute 간의 종속 관계를 분석하여 여러 개의 relation으로 분해(decomposition)
→ 정규화
* 단, decomposition이 정규화는 아니다.
* decomposition을 통해 문제가 해결되어야 정규화라고 할 수 있다.
[ 중복성에 따른 여러 문제 ]
· 중복성은 관계 스키마에서 발생하는 여러 문제의 근본적인 원인이다.
· 무결성 제약 조건, 특히, 함수 종속성(Functional Dependency)를 분석하면
문제가 있는 스키마을 파악할 수 있다.
· 주된 정제 기법 : 분해(decomposition) ex) ABCD를 AB/BCD or ACD/ABD로 대체
* 분해는 이유없이 하지 않는다.
* 분해로 인해 또 다른 문제 발생하지 않도록 주의한다.
[ 함수 종속(Functional Dependency) ]
· table에서 프로젝트 연산 수행 시 속성 x의 x1에 해당하는 속성 y가 모두 y1 일 때 함수 종속이 존재한다고 간주한다.
ex) pk(primary key)는 다른 모든 attribute에 대해 함수 종속이 존재한다.
→ pk가 정해지면 튜플이 특정되기 때문이다.
· 즉, table 내에 FD는 항상 존재하지만 그 속에서 문제를 찾아내야 한다.
[ 기본 정규형 ]
· 정규형(Normal Form)
- 어떤 일련의 제약조건을 만족하는 relation
· 정규화의 원칙
1) 무손실 표현
- 원래있던 정보가 정규화로 사라지면 안된다.
→ 같은 의미의 정보를 유지하되 더 바람직한 구조를 가지도록 한다.
2) 데이터의 중복성 감소
3) 분리의 원칙
- 독립적인 관계는 별개의 relation으로 표현한다.
- relation 각각에 대해 독립적 조작이 가능하다.
[ 제 1 정규형(1NF) ]
정의 : 모든 도메인(attribute)가 원자값으로만 이루어진 relation

# 위 1NF에서의 이상
1) 삽입 이상
- 400번 학생의 지도교수가 p4라는 것을 교과목 수강없이 삽입 불가
2) 삭제 이상
- 200번 학생이 c2 수강 취소 시 이 튜플이 삭제되면 p2 지도교수의 정보도 사라진다.
3) 갱신 이상
- 300의 지도교수를 p1으로 변경하려면 300에 해당되는 모든 튜플을 갱신 해야한다.
# 이상 원인
- 기본키에 부분함수 종속 된 attribute가 존재한다.
- 기본키로 식별되는 개체와 문관한 attribute가 존재한다.
- 두 가지 상이한 정보가 포함되어있다.
# 이상 해결 : 프로젝션을 통해 relation을 분해하여 부분함수 종속을 제거한다. → 2NF
[ 제 2 정규형(2NF) ]
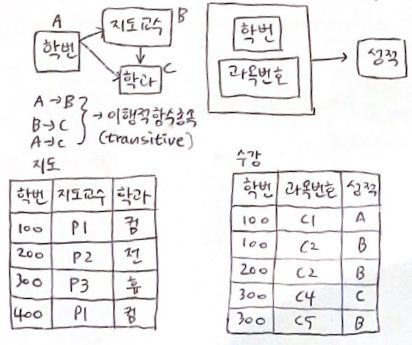
정의 : 1NF 이고 키에 속하지 않는 attribute들은 모두 기본키에 완전 함수 종속이다.
# 오른쪽 2NF에서의 이상
1) 삽입 이상
- 교수 p4가 컴과에 속한다는 사실을 삽입하기 위해서는 반드시 지도 학생이 있어야 한다.(지도학생이 없으면 삽입 불가)
2) 삭제 이상
- 300번 학생이 졸업해 튜플이 삭제 될 경우 지도 교수 p3가 휴먼과에 속한다는 정보가 사라진다.
3) 갱신 이상
- 지도교수 p1의 전공이 변경되면 관련 튜플을 모두 갱신 해야한다.
# 이상 원인 : 이행적 함수 종속이 존재한다.
# 이상 해결 : 프로젝션으로 relation을 분해하여 이행적 함수 종속을 제거한다. → 3NF
+) attribute가 2개면 무조건 제 3 정규형이므로
( 학번-지도 / 지도-학과 ) or ( 학번-학과/지도-학과 )
→ 위 둘 중 어떻게 relation을 분해해도 제 3 정규형을 만족시킨다.
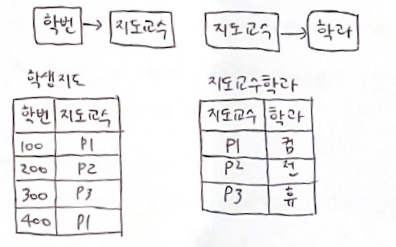
[ 제 3 정규형(3NF) ]
정의 : 2NF이고 키가 아닌 모든 attribute들은 기본키에 이행적 함수 종속 되지 않는다.
[ BCNF ]
정의 : relation R의 모든 결정자가 후보키이면 relation R은 BCNF에 속한다.
| * 후보키 : 튜플을 유일하게 식별할 수 있는 키가 여러 개 인 경우, 키가 될 수 있는 후보가 여러 개라고 간주할 수 있다. 따라서 키가 될 수 있는 것을 후보키라 부름. * 결정자 : FD에서 화살표가 출발하는 쪽을 결정자라 부른다. ex) 오른쪽 relation에서의 FD - 과목이 교수에 의해 결정되므로 교수는 결정자이다. - 교수는 {학번, 교수}의 집합을 통해서만 유일하게 결정되므로 {학번, 교수}는 결정자이다. |
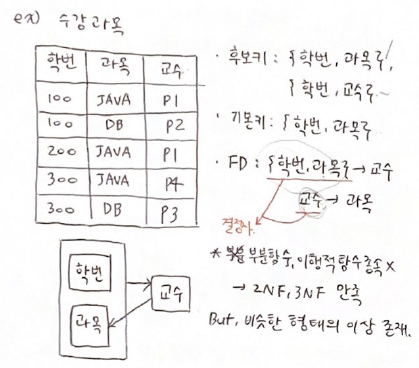 |
# 위3NF에서의 이상
1) 삽입 이상
- 교수 p5가 특정 과목 담당을 위해서는 이를 수강 할 학생이 필요하다.(수강 학생이 없으면 교수가 과목 담당 불가)
2) 삭제 이상
- 100번 학생이 DB과목 수강을 취소하면 p2가 DB를 강의한다는 정보까지 사라진다.
3) 갱신 이상
- 교수 p1이 JAVA 대신 다른 과목을 담당하면 모든 관련 튜플을 갱신해야한다.
# 이상 원인 : 교수가 결정자이지만 후보키가 아니다.
# 이상 해결

[ FD 좀 더 살펴보기]
# Armstrong의 공리 → 증명할 필요없이 당연한 것
· 반사(Reflexivity) : X⊆Y then X→Y ex) { 학번, 교수 } ← 학번
· 첨가(Augmentation) : X→Y then XZ→YZ
· 이행(Transitivity) : X→Y and X→Z then X→Z

· 결합(Union) : X→Y and X→Z then X→YZ
· 분해(Decomposition) : X→YZ then X→Y and X→Z

# 분해에 따르는 문제
1) 어떤 질의는 처리 비용이 더 높아진다. ex) 조인 연산
2) 분해한 relation의 instance들로부터 원래 relation을 재구성할 수 없는 경우가 생기기도 한다.
3) 어떤 종속성을 체크하려면 분해된 instance들을 조인해야하는 경우가 존재한다.
*Trade-off : 이러한 문제들과 중복성 간의 타협점을 찾아야한다.
[ 제 4 정규형(4NF) ]
정의 : relation R에서 MVD(다치 종속성) A -->>B 가 존재할 때 R의 모든 attribute들이 A에 함수 종속이면 R은 4NF이다. 즉, R의 모든 attribute X에 대해 A→X 이고 A가 후보키.
BCNF를 이용한 정의
: relation R이 BCNF에 속하고, 모든 MVD가 FD이면 F은 4NF이다.

· 의미
- 어떤 relation R이 4NF이려면 MVD가 없거나, A -->>B|C가 있는 경우, A에 대응되는 B와 C의 값은 하나 씩이어야하며 이때 A는 후보키임을 의미한다.

[ 제 5 정규형(5NF) ] →n분해 relation(조인종속)
· n-분해 relation : n개의 프로젝션으로만 무손실 분해가 가능하다. → n개 미만으로는 불가능
정의 : relation R에 존재하는 모든 조인 종속이 R의 후보키를 통해 성립되면 R은 5NF이다.
[ 역정규화(Denormalization) ]
역정규화란?
- system의 성능 향상을 위해 정규화에 위배되는 행위를 하는 것이다.
- 성능 향상을 위해 정규화 무시
· 역정규화 고려사항
- 업무에 따른 데이터 사용량(입력, 수정, 조회, 삭제)과 업무 프로세스 분석
ex) 학교 table 중 프로세스 비율을 가장 많이 차지하는 것은 갱신과 조회가 매우 빈번한 수강 table이라고 할 수 있다.
[ 역정규화 유형 ]
1) 데이터 중복(컬럼 역정규화)
- 조인 프로세스를 줄이기 위해 조인으로 조회하는 컬럼을 중복하여 기본적으로 조인 연산을 수행하지 않도록 한다.
- 조회가 자주, 많이 일어나는 table은 이를 통해 성능 향상을 기대할 수 있다.
2) 파생 컬럼 생성
- 조회할 때마다 숫자 연산이나 데이터 조작을 통해 결과를 얻는 컬럼을 포함하도록 한다.
ex) 평점 → 전체 학점을 더해 평균을 내야한다. 평균 연산을 줄이기 위해 평균 평점 컬럼을 미리 생성.
3) 3NF 2개 → 2NF 1개 (이행적 함수 종속을 제거하지 않는 방법)

< 테이블 분할 , 합병 >

· Vertical Partition
- 컬럼을 기준으로 분리
- 업무적인 내용을 분석하며 조회 시 질의 안에 포함되는 컬럼들을 중심으로 컬럼을 나눈다.
· Horizontal Partition
- record(row, tuple)을 기준으로 분리
- 높은 빈도수와 낮은 빈도수에 따른 record 분리 ex) 우수 고객 관리
- 빈도수 상관없이 데이터 성격에 따른 record 분리 ex) 거주 지역에 따른 분리
'4-1 > 데이터모델링과마이닝' 카테고리의 다른 글
| [데이터모델링과마이닝] 8. 데이터 마이닝(Data Mining) (0) | 2022.07.18 |
|---|---|
| [데이터모델링과마이닝] 6. 논리설계와 관계 데이터 모델 (0) | 2022.07.16 |
| [데이터모델링과마이닝] 5. DBMS 설계 상의 선택들 (0) | 2022.07.14 |
| [데이터모델링과마이닝] 4. ER 모델의 고급 기능 (0) | 2022.07.14 |
| [데이터모델링과마이닝] 3. 개념 설계와 ERD (0) | 2022.07.14 |




