| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 프로그래머스 완전탐색
- react hook
- 리액트 훅
- 코딩테스트 고득점 Kit 완전탐색
- 프로그래밍 언어론
- 백준
- 컴퓨터 네트워크
- 프로그래머스
- react firebase
- NextJS
- websocket
- react
- 자바 공부
- codesandbox
- 자바스크립트
- Java
- React JS
- useState
- 리액트
- 코틀린
- 코딩테스트 고득점 Kit
- design pattern
- 장고
- vanillaJS
- 자바
- JavaScript
- 디자인 패턴
- 데이터모델링과마이닝
- useEffect
- 프로그래머스 자바
- Today
- Total
기록하는 개발자
[백준][JAVA] 11729 : 하노이 탑 이동 순서 본문
https://www.acmicpc.net/problem/11729
11729번: 하노이 탑 이동 순서
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로
www.acmicpc.net

하노이탑
하노이탑 문제는 전공 수업 때도 배우는만큼 굉장히 유명한 공식이다.
하노이탑의 가장 큰 규칙은 아래 두 가지로, 두 규칙을 지키면서 다른 기둥으로 옮기기 위한 과정을 수열로 표현해보자.
1. 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
2. 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
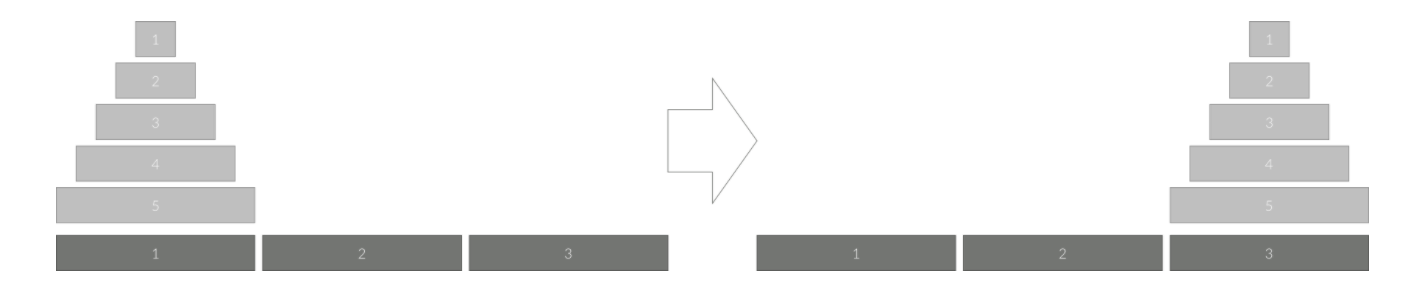
세 개의 장대 위에 n개의 원판이 쌓여있다. 각 원판은 반경이 큰 순서대로 쌓여있으며 첫 번째 장대에서 세 번째 장대로 모두 옮기고자 한다.
1. 가장 큰 원반인 n번 째 원판을 장대3으로 옮기기 위해서는 n-1 개의 원판을 장대1에서 장대2 로 옮겨야한다.
- n-1개의 원판을 장대2로 이동해야하므로 장대1에서 장대2로 보내는 행위를 n-1번 반복 해야한다.
- 장대1에서 장대2로 보내는 행위를 Hanoi라는 함수가 수행한다고 가정한다면 총 이동 횟수는 Hanoi(n-1)번이다.
2. 장대1에 남은 n번째 원판을 장대3으로 옮긴다.
- 현재 1부터 n-1까지의 원판은 모두 장대2에 올라가있다. 따라서 n번째 원판을 장대1 에서 장대3으로 옮기기만 하면 된다.
- 위 행위를 통한 이동횟수는 1번 이다.
3. B 에 있는 (n-1)개의 원판을 C 로 이동한다.
- 1번에서 장대1에서 장대2로 n-1개의 원판이 이동했던 것과 동일하게, 장대2에서 장대3으로의 총 이동 횟수는 Hanoi(n-1)이다.
위 1~3번을 공식화 해보면 Hanoi(n) = Hanoi(n-1)*2+1 로, 일반항은 2ⁿ-1이 된다.
수학적 귀납법을 이용한 자세한 설명 참고 : https://lgphone.tistory.com/106
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
public class Main {
public static StringBuilder sb = new StringBuilder();
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
sb.append((int)(Math.pow(2,N)-1)).append('\n');
Hanoi(N, 1, 2, 3);
System.out.println(sb);
}
public static void Hanoi(int N, int start, int mid, int arrive) {
if (N == 1) {
sb.append(start + " " + arrive + "\n");
return;
}
Hanoi(N-1, start, arrive, mid);
sb.append(start+" "+arrive+"\n");
Hanoi(N - 1, mid, start, arrive);
}
}
'Algorithm' 카테고리의 다른 글
| [프로그래머스][JAVA] 숫자 문자열과 영단어 (0) | 2022.05.03 |
|---|---|
| [프로그래머스][JAVA] 키패드 누르기 (0) | 2022.05.03 |
| [백준][JAVA] 1697 : 숨바꼭질 (0) | 2021.10.07 |
| [백준][JAVA] 7576 : 토마토 (0) | 2021.10.06 |
| [백준][JAVA] 9935 : 문자열 폭발 (0) | 2021.09.11 |




